
おまけ問題の解答
1=2であることを証明しなさい。
a = a
![]()
![]()
ここで、中学校のときに習った因数分解を思い出してください。
![]()
でしたよね。
ですから、
![]()
となります。
左辺をaでくくります。
![]()
(a-a)が両辺にありますから、切ります。
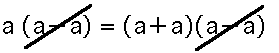
![]()
![]()
で、左辺と右辺にaがありますから、切ります。
![]()
![]()
はい。できあがり (笑)
これができても・・賞品はありません。ごめんなさい。
「1=2」証明問題の解答の解答、そしてコメント
解答の解答
この証明問題に正しい解答を寄せてきた読者が多いので、びっくりしました。プライベートで遊んでいた時には100人に一人の正当率でしたが、それを確実に上回ります。
ちなみに、メールで解答して頂いた方は20人程度ですから、読者数、約7,000人に対しての正当率は1%をはるかに下回りますが、サイレントマジョリティの存在を考えると、軽く2〜3%を越えることでしょう。
秘密は(a−a)が両辺にあるので「切る」行為のところです。
(a−a)はゼロです。そして「切る」というのは、その数字で両辺を「割る」という意味です。
つまり、上の証明問題の模範解答では、ゼロで割ってしまったところに問題があるのです。
数学の世界では、ゼロで割ることができないとされています。これはルールです。
だから、解答は実は「間違い」です。
(間違いでなければ1=2が証明できてしまいますから、当たり前ですが(笑))
「1=2」だって、いいじゃないですか
素朴な疑問があります。
なぜ、「ゼロで割ってはいけない」のでしょうか?
確かにいろいろと大学でも習いました。数学といってもほとんど哲学の世界です。
でも結局私には、「ゼロで割ってはいけない」のは「1=2」が証明できてしまうからとしか思えません。
「1=2」を認めてしまうと「1+1=2」ではなく、「1+1=3」や「1+1=4」になってしまいす。数学の根幹が揺らいでは話になりません。だから、ムリヤリ「ゼロで割ってはいけない」というルールを作った。私にはそうとしか思えません。
でも、本当にそうなのでしょうか。「1=2」ではいけないのでしょうか。
小学生に算数を教えるとき、こんな感じで例を出します。
そこに女の人が1人やってきました。
さて、何人でしょう?」
たまに、「3人!!」と元気な声が返ってきます。
「子どもが生まれるから」がその理由(笑)
ある宣教師がアフリカの原住民に算数を教えようとして例を出しました。
ライオンが1匹やってきました。
さて、何人(匹)でしょう」
「1+1=2」をちゃんと習ったのにも関わらず、全員「1人!」と答えます。
「ライオンが人間を食べてしまうから」が理由。
これらの例は笑い話として語られることが多いのですが、それだけで済ませて良いのでしょうか。「3人」と答える子どもを「こまっしゃくれたガキだ」と決め付けて良いものなのでしょうか。
確かに、こどもには「1+1=2」はきちんと教えてあげなければいけません。
でないと実生活で混乱するからです。
中学2年生の時に「1=2を証明せよ」という証明問題にぶつかった子どもは、こんな皮肉なヤツになります(←私のことです(笑))
でも、現実社会では「1+1」は3になったり1になることも多いのです。
同じことがユークリッド幾何学と非ユークリッド幾何学にいえます。
私たちが学校で勉強するのは主にユークリッド幾何学です。これは2次元の世界を前提としています。非ユークリッド幾何学は3次元。
従って、
はユークリッド幾何学でしか言えません。
球体、つまり、地球上に描かれた三角形は180度を越えてしまいます。
いや、すでにそれはユークリッド幾何学では三角形ですらありません。曲線でできているからです。
という定義も、東京から北へ「直線」を描き、一方はニューヨークから「直線」を描くと北極で交わってしまいます。そう、非ユークリッド幾何学には「直線」という概念はありません。
私たちは当然のことながら、非ユークリッド幾何学の世界に棲んでいます。
現実の世界のことは学ばずに、現実とは違う世界の話を信じる。
良く考えてみれば、ちょっと怖いことです。
「1=2だっていいんじゃないか」と受け入れてみる柔軟性は、マーケティングでは大きな武器になることが多々あります。
「1+1=2」は確かに便利です。私たちの生活では、このことを信じないと都合が悪いことが多くなります。
でも、数字に振り回されないことも大切です。
という方には特に「1=2」をオススメします。
【おまけ話】
数学の次は物理学です(笑)
ゼロ次元は点の世界。点が動いた跡は線になり、これが1次元。
線が動くと面となり、2次元になります。
そして、面が動くと立体で、3次元になります。
で、立体が動くと・・・立体のままじゃないですか(笑)
理屈でいえば、動くと時間が経過するから、
ということは知っていますが、目に見えないから実感が湧きません。
また、点や面が動くときには時間は加味されないのに、立体が動くときだけ時間を足すのも良くわかりません。
私の頭では理解できないことがあるのでしょう。
というのも、それぞれの次元での人間はこんな感じだろうからです。
線しか存在しない1次元の世界に人間が住んでいるとします。
一方から歩いてきたA君は他方から歩いてきたB君とぶつかってしまうと、にっちもさっちも行きません。1次元の世界には直線の概念しかないからです。
でも、面で構成されている2次元世界の人間C君から見れば「バカなヤツだよな。横に回れば良いのに」と思います。
今度は、2次元の世界で大きな金庫を作るには、四角で囲んでしまえば事足ります。
そして、四方に警備員を配置すればおしまい。
2次元の住人にとっては「高さ」という概念がないからです。
ところが、3次元の住人D君にとって、その金庫からお宝を盗むのは簡単です。上からひょいとお宝を取れば良いだけです。
4次元や5次元の世界に住人がいるとすると、私が「立体を動かしたって立体じゃないか」と騒いでいるのを見て、せせら笑っていることでしょう。
アメリカで真剣にタイムマシンを作っている、いや研究している大学があります。
理論的には製造可能なのです。
是非、乗ってみたいんです。タイムマシン。
そこで、江戸時代の江戸の町、特に町人文化をこの目で見てみたい、というのもありますが(すみません。唐突で(笑))、4次元の住人に会って彼らの「常識」を聞いてみたいのです。
発想の枠が広がるようでワクワクするじゃないですか。
中学生のときにショックを受けた「1=2」。それを肯定するか否定するか、それは、私の中ではどうでも良い問題になっています。
数字のプロと見られるコンサルタントですが、最後は、生活者に夢を与えられるかどうか、クライアントに夢を持ってもらえるかどうか。それが、私たちの使命だからです。